Solving Systems of Linear Equations with Row Reduction on the TI-83 Plus and TI-84 Plus

Suppose you wanted to find the solutions to the following set of equations:

Xavier and Yolanda both bake pies. In one hour, the pair create a total of 5 pies. If Xavier works for 3 hours and Yolanda works for 4 hours, the pair can create a total of 17 pies. How many pies does each produce per hour?

This tutorial discusses how to solve such problems, and a clever trick to make even the hardest linear simultaneous equations easy.

To solve our problem, we can set up a system of equations. Let x be the amount of pies Xavier makes in an hour, and y be the amount Yolanda makes in an hour. Then we know that:

x + y = 5

3x + 4y = 17

To solve this problem, note that 3x + 3y = 15. Subtracting this from the second equation, we have y = 2. Since x + y = 5, x must equal 3. So Xavier produces 3 pies in an hour and Yolanda produces two.

This problem seems simple enough, but would be much harder if, for example, we had 5 people making pies, or the numbers didn’t work out evenly. This tutorial explains how to solve such systems of equations using your TI-83 Plus or TI-84 Plus calculator.

Row Reduction

The basic idea behind row reduction is to create a standardized way of solving systems of linear equations. Let’s take a look at the following problem:

x + y = 2
3x + 4y + z = 17
x + 2y + 3z = 11

To begin the process of row reduction, we create a matrix consisting of the numbers in our linear equation.
Since there is no “z” term in the first equation, we rewrite it as 0z before continuing.

1	1	0	2
3	4	1	17
1	2	3	11

Note that the variables must be in the same order before this conversion, otherwise there is an ambiguity. Therefore, if we had written:

x + y = 2
4y + z + 3x = 17
2y + x + 3z = 11

we would have to rewrite it before performing this step.

Now that we have our matrix, we begin the process of row reduction. With row reduction, each operation done is
on the rows, and there are three basic operations we can do:

1. Add or subtract a multiple of any row from any other row
2. Multiply any one row by a constant
3. Swap any two rows

The goal of row reduction is to get only one nonzero term in each of the first three rows.

Step 1: Reaching Upper Triangular Form

First, we want to modify the matrix until it is in what is called “upper triangular form.” This just means that all the nonzero terms are in the upper triangular piece of the “coefficient” matrix, the part that originally contained the coefficients of the x, y, and z terms in our equation. What this means will become clearer once we are there.

Let’s begin by swapping the order of the rows into one more convenient for solving our problem:

1	2	3	11
1	1	0	2
3	4	1	17

Now let’s subtract three times the first row from the third row.

1	2	3	11
1	1	0	2
0	-2	-8	-16

Next let’s subtract the first row from the second row.

1	2	3	11
0	-1	-3	-9
-0	-2	-8	-16

Now we only have one term in the first column. Let’s multiply the second and third rows by -1.

1	2	3	11
0	1	3	9
0	2	8	16

Let’s subtract two times the second row from the third.

1	2	3	11
0	1	3	9
0	0	2	-2

We are now in upper triangular form. Were we to convert our matrix back to a system of linear equations, it would read:

x + 2y + 3z = 11
y + 3z = 9
2z = -1

Step 2: Solving for Variables

It is clear why this form is useful – we can now solve for z, subtract it from the term containing only y and z, and then solve for y and so forth. Let’s continue by dividing the third row by two.

1	2	3	11
0	1	3	9
0	0	1	-1

Now we can subtract three times the third row from the second and first rows:

1	2	0	14
0	1	0	12
0	0	1	-1

Finally, subtract twice the second row from the first row:

1	0	0	-10
0	1	0	12
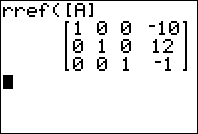
0	0	1	-1

Converting back to equation form, we have x = -10, y = 12, and z = -1. You make have realized that the process of row reduction is more or less what we had originally did with our simpler problem, and this is exactly the case. Row reduction is simply a more standardized and cleaner method of solving systems of linear equations.

This seems tedious, and it is, especially as we add more and more variables, but don’t worry, your calculator can perform the same operation while saving you a lot of the dirty work.

Row reduction on the TI-83 Plus and TI-84 Plus

To perform row reduction on your calculator, we just have to perform the first step, converting your equations into a matrix.

As before, we can convert:

x + y = 2
4y + z + 3x = 17
2y + x + 3z = 11

into:

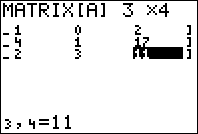
1	1	0	2
3	4	1	17
1	2	3	11

From your calculator’s home screen, just press 2nd x^-1 to select the MATRIX menu, then press ▶ ▶ .

Select an empty matrix using the arrow buttons, or else one you don’t mind overwriting, and press ENTER .

Next, enter the matrix dimensions. These are measured as # of rows by # of columns, so press 3 ▶ 4 ▶ to enter the correct dimensions for our matrix. To enter each number, select the correct slot using the arrow buttons, enter the number, and press ENTER to confirm.

Once you are done filling out your matrix, return to the home screen by pressing 2nd MODE. Return to the matrix menu by pressing 2nd x^-1, press > to select the MATH submenu, and use the arrowkeys to select rref(. Press ENTER to paste this command to the home screen. Next return to the matrix menu by again pressing 2nd x^-1, use the arrow buttons to select the name of the matrix you entered your data in, press ENTER to paste it to the home screen, and ENTER again to evaluate the command. Your calculator will display the reduced matrix, from which you can read off the solutions to your equation.