Derivatives are perhaps the most elementary topic in calculus and show up in practically every discipline, from the natural and social sciences to economics and finance. This tutorial discusses the mathematical background of derivatives and demonstrates how to evaluate derivatives on the TI-83 Plus, TI-84 Plus, TI-89, TI-92 Plus, and Voyage 200.
Mathematical Background
The derivative of a function is its slope at a particular point. Just like the slope of a line is rise over run, or change in y divided by change in x, the derivative of a function is calculated by looking at the change in y divided by the change in x, except looking at only a very small slice of a function at a time. In general,
![]()
The prime (‘) symbol is just another way to denote a derivative. The derivative of a function g(x) can be written as g'(x). dy and dx are differentials, which basically means a very small slice of a function at a particular place. dy means “change in y over a small piece” and dx means “a small change in x.” The process of calculating a derivative is called differentiation. Sometimes the independent variable (the y in this case) is omitted and the derivative is written simply as d/dx. (Change in function value per small change in x.)
Of course, the derivative of a function is also a function because it is typically different at different points along the original function. For example,
![]()
This means at x=0, the derivative of the function y=x² is 0–which makes sense, because the function is flat there. However, at x=2, the derivative is 2*2=4. At this point on the curve, it slopes upwards, hence a positive derivative.
Another way of looking at a derivative is the slope of a tangent line at a specific point. A tangent line is a line which touches a function without crossing it at a specific point. Finding a tangent line to a curve is one of the most elementary uses of the derivative.

This image shows the derivative at various points as the slope of a tangent line. When the derivative is positive, the line is green. When the derivative is negative, the line is red. When it is zero, the line is black.
Derivatives on the TI-83 Plus and TI-84 Plus
On the TI-83 Plus and TI-84 Plus, from the home screen press to select the nDeriv function.

The nDeriv function is located on your device's MATH menu.
After the nDeriv function is pasted to your home screen enter the arguments for the function: First, enter the function you want to differentiate (for example, if you want to find the derivative of y = sin(x), enter sin(x)) then press , enter the variable of your function, press again, and enter the x coordinate you want to evaluate the derivative at. Press to evaluate.
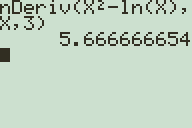
The actual value is 5 and 2/3, but the calculator uses the definition of the derivative as (change in y/ change in x) to calculate it at a point, and isn't always accurate to the last digit.
Unfortunately, this function only returns the derivative of a single point. While there is no built-in function on the TI-83 Plus and TI-84 Plus to take a derivative in general, you can read more about using an application to enable this functionality here.
Derivatives on the TI-89, TI-92 Plus and Voyage 200
From the home screen, press and “d( differentiate” should be the first function listed. Press to paste it to the home screen.
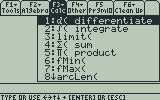
The differentiate function is located on your device's Calc menu.
Next, enter the function you want to differentiate, press , enter the function variable, and add a closing parenthesis to finish the expression. Press to evaluate.
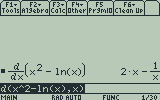
The TI-89, TI-92 Plus, and Voyage 200 evaluate derivatives symbolically.
Instead of calculating a specific value, the calculator displays a general expression for the derivative. If you’re interested in evaluating the derivative at a different point, before pressing on your expression, type , the variable you want to evaluate the derivative for, , and then the numeric value. Press and your calculator will display the value at the point you entered.
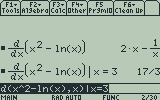
You can also specify a specific x value to calculate the exact value of the derivative at a single point.
You can also do this after the fact by pressing to clear the input line, pressing to select the output of your derivative calculation, pressing to paste it into the input, and then typing the same syntax (for example, “|x=3”) as above after the expression.
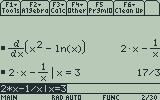
You can also select the output of the derivative function to evaluate it at a single point.
The TI-89, TI-92 Plus and Voyage 200, also have an nDeriv function like that on the TI-83 Plus and TI-84 Plus, but there are few cases where such a function is more useful than the differentiate function.

One Response to Calculating Derivatives on the TI-83 Plus, TI-84 Plus, TI-89, TI-92 Plus, and Voyage 200