The limit of a function is a fundamental calculus concept which is used in characterizing functions, calculating derivatives, and more. This tutorial discusses the theory of limits and how to evaluate limits, including left and right-handed limits, on your TI-89, TI-92, or Voyage 200 calculator.
Mathematical Background
The limit of a function at a particular point is the value a function gets close to as it approaches that point. This does not mean the function has the same value at that point, or even that the function exists at that point. For example, if we take:
![]()
We can’t actually evaluate the function at the point x = 2 because we would be dividing by zero. However, since x² – 4 = (x + 2)(x – 2), we can cancel the (x – 2) terms and evaluate the limit as:
![]()
The actual function itself looks exactly like the line y = x + 2 except at the point x = 2, where it doesn’t exist. However, we can still evaluate the limit at this point, since if we look at points just to the right or left of x = 2, the values get closer and closer to 4.
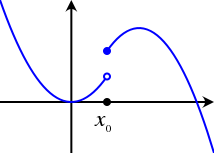
One way of defining the limit of a function at a point is that as you approach that point from any direction, you get the same limit. For functions in one variable, we have only two directions to approach a point from: either from the positive or the negative sides. For example, the following function does not have a limit at x = x₀.
Functions can also have a limit as they go to plus and minus infinity. This simply means, as above, that as the function is evaluated at larger and larger or smaller and smaller numbers (towards positive and negative infinity), the function becomes closer and closer (or approaches) a specific value. For example:
![]()
As we substitute larger and larger numbers for x (towards positive infinity) for the function 1/x, the result becomes closer and closer to 0.
Evaluating Limits on Your Calculator
To enter the limit function on your TI-89, TI-92, or Voyage 200, from the home screen press . This pastes the limit( function to your home screen. Then enter the function you want to evaluate the limit of, press , the independent variable of the function (usually x), again, the point at which you want to evaluate the limit, and finally press to add a closing parenthesis and press to evaluate.
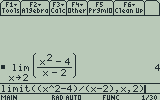
The general syntax is limit(function, variable, point).
To evaluate left and right-handed limits, before adding a closing parenthesis, press again and enter -1 for a left handed limit or 1 for a right handed limit. Finish by pressing to add a closing parenthesis and evaluate. The syntax becomes limit(function, variable, point, left/right handed sign).
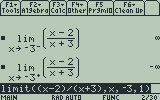
The output represents the fact that as you approach the function at x=3 from the left side, it becomes infinitely large, whereas if you approach the function at x=3 from the right side, it becomes infinitely small.
As with all functions, the TI-89’s limit function draws upon the calculator’s symbolic math functions. Experiment around and see what else is possible!
