Algebra Mini-Series #5: Fraction Mistakes, Cross Multiplying, and Solving Rational Equations

This is the final installment of our weeklong series on improving your algebra skills. Our goal for this series was to provide a useful resource for both students and teachers, so that this article can be used in the classroom, for test prep, or to help yourself practice and master skills you never learned. We hope you’ve found this helpful, and that we can do more series like this one in the future.

Back to: Part 4: How and When to Multiply in Algebra

Five Tricks to Improve Your Algebra Skills

Part 5: Common Fraction Mistakes and Clearing Denominators

An old joke reads “4/3 of people have trouble with fractions.” Of course, were this really true then nobody would get the joke, but there is unfortunately a lot of truth in this witticism nonetheless. If I had a dollar for every time I’ve seen a student in precalculus and beyond mess up a problem because they don’t know how to deal with fractions, I would be a very rich man.

Which this in mind, I urge all teachers of math to spend their first class each term “re-teaching” students how to use fractions. Chances are, at least a third of your class is not really comfortable with fractions at all, and most of the other students could at least use a refresher. In this light, this article isn’t really about learning anything new per se. Instead, it focuses on a few of the things about fractions many students aren’t familiar with (even though they should be), and then on clearing denominators to solve equations with fractions.

Common Fractions Mistakes

Mistake: Not Multiplying Through

Problem:
3 * (x+2)/(x-4) = ?

Incorrect Method:

Correct Method:

I’ve often seen this mistake in cases where students understand perfectly how to distribute, but somehow dealing with fractions scares them to the point of not knowing what to do with the factor of 3.

Mistake: Splitting Up Fractions Incorrectly

Problem:
(3x + 2)/(3x + 3) = ?

Incorrect Method:

Correct method:

This mistake is also extremely common. The cause is simply unfamiliarity with fractions so that rules of multiplication and addition become confused.

Mistake: Dividing Fractions by Nested Fractions Incorrectly

Problem:
2/(4/3) = ?

Incorrect Method:

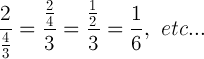
Correct Method:

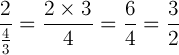
This one is also often missed by students, usually because it isn’t in the typical form of (a/b) / (c/d), which more students solve correctly. It’s best to review both of these, especially if students are going to be working with rational equations.

Mistake: Not Knowing How to Deal With Negative Signs in Fractions

Problem:
2/-4, -3/7, etc…

Correct Method:

This is absolutely fundamental, though many students still don’t understand this. If you’re a student, make sure you know this one—it’s as often missed as the ones above, but is absolutely crucial to good algebra.

Other important topics to review include factoring and dividing numbers and expressions and rationalizing denominators using conjugates, since these too are often missed despite their usefulness.

Solving Rational Equations by Clearing Denominators

The easiest way to teach solving rational equations is by clearing denominators. Take the following for example:

Solve for x:
1/(x-1) – 1/(x+1) = 1/(x)

Solution: Multiply all terms by (x-1)(x+1)(x) and expand. This gets rid of all equations and turns the problem into a polynomial equation:

(x+1)(x) – (x-1)(x) = (x-1)(x+1)
x² + x – x² + x = x² -1
2x = x² – 1
x² – 2x – 1 = 0

By the quadratic formula, x = 1 +/- √(2)

For simple equations consisting of only two terms, clearing denominators can easily be condensed into the mnemonic of “cross multiplication:”

While it’s useful as a student to understand this technique, the ultimate goal of course is not to learn to solve such equations by rote memorization. The ultimate goal should be the same as always: to develop a problem solving skillset aimed at isolating relevant quantities to get equations into a form easy to solve.