SAT Test Prep #3: Calculating Sale Prices, Percentages and Discounts

One of the ways you can improve your SAT is score is identifying problems that may seem simple but are actually written to trick you. If you are rushing through a test, you may miss out on easy points. Consider the following, seemingly simple problem:

A dress is on sale at a clothing store. During the discount sale its price is reduced by 40%. Staff are allowed a further 30% reduction on the discounted price. If a staff member buys the dress for 42 dollars, what was the original price of the dress, in dollars?
(A) $71.40
(B) $76.44
(C) $82.00
(D) $88.25
(E) $100.00

How do you find the price of the dress? Pick you answer and keep reading to find out how to solve the problem!

This SAT question seems pretty easy, right? You may be tempted to add the 40% to the 30%, multiply the $42 by 1.70 (for 170% of the price paid), and come up with answer (A), or a price of $71.40. Unfortunately, this is not the correct approach. So what is the first step to solving this problem?

Re-reading the problem, we know there is an original price for the dress, before any discount is applied. Our goal is to find this original price. We know that:

• The price paid for the dress is $42
• $42 is the price after a 30% discount
• Before the 30% discount is applied for a final price of $42, the price of the dress is discounted 40% from the original price

Given this information, here is how we get from the original price to $42:

Original Price > 40% Discount > Price before Staff Discount > 30% Discount > $42

Since the original price is unknown, we’re going to make it a variable. We’ll use x to represent the original price for simplicity. We know that our original price x is discounted by 40%. If x is discounted by 40%, the price after the discount is 60% of the original price. If the starting price is 100% of the current value, we subtract a 40% discount for a value of 60% of the starting price, or (1 – .40) = .60.

This brings us to the price after the 40% discount. To get to a final price of $42 for the dress, we discount the price after the 40% by an additional 30%. Essentially, the final price of $42 is 70% of the intermediate price (after the 40% discount).

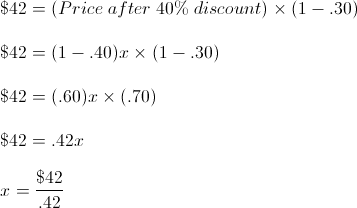
Solving for x, we find that the original price of the dress before any discounts is $100, or answer (E).

Solving on your Graphing Calculator

Now that we have an idea of how to approach the problem, here is how you can easily solve it on your graphing calculator:

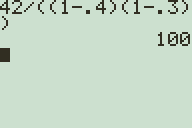
All you have to do to solve this problem is to multiply 60% of the original price (representing the 40% discount), by 70% of the price with the 40% discount (reflecting the 30% discount), dividing this value by the final price of $42 to find the original price. We can check our work once we have found the original price by working backwards:

• $100 times 60% or .60 = $60
• $60 times 70% or .70 = $42

The simple way to solve this type of problem is:

• (1 – First Discount) × (1 – Second Discount) × (Original Price) = Final Price
• (1 – .40) × (1 – .30) × Original Price = $42
• .42 × (Original Price) = $42
• Original Price = $42 ÷ .42

Divide the final price by the product of your discounts, and you’ll find the original price. The key to succeeding on the SAT is to spend a few seconds thinking about the problem, writing down the steps needed to reach the solution, and then double-checking your answer to make sure your method is correct. This way you won’t miss out on important points that are easy to earn!